For many beginner programmers, the idea of data structures can be confusing. Questions like "Why do we need them?" or "Why focus on this when there are other topics?" often come up. However, in reality, data structures form the foundation of programming.
Essentially, programming involves working with information using rules, or algorithms. And what about data? It's simply the information stored in a computer's memory. Sounds simple, doesn't it? But computers aren't perfect.
The speed at which we can perform these tasks depends on how the data is organized in memory. And that's where data structures come into play. They decide how data is organized.
Most programming languages already provide ways to handle data using these structures. Some structures are built on top of others, so it's good to learn them step by step.
In this blog, we focus on a basic data structure: the array. We will delve into its workings to understand how it operates.
Array
An array is a data structure that consists of a collection of elements (values of different types or the same type), each identified by at least one array index. Imagine them as a lineup of boxes, each arranged one after the other, containing a piece of information, which makes it easy to access and manipulate the data they hold.

Dimensions in Arrays:
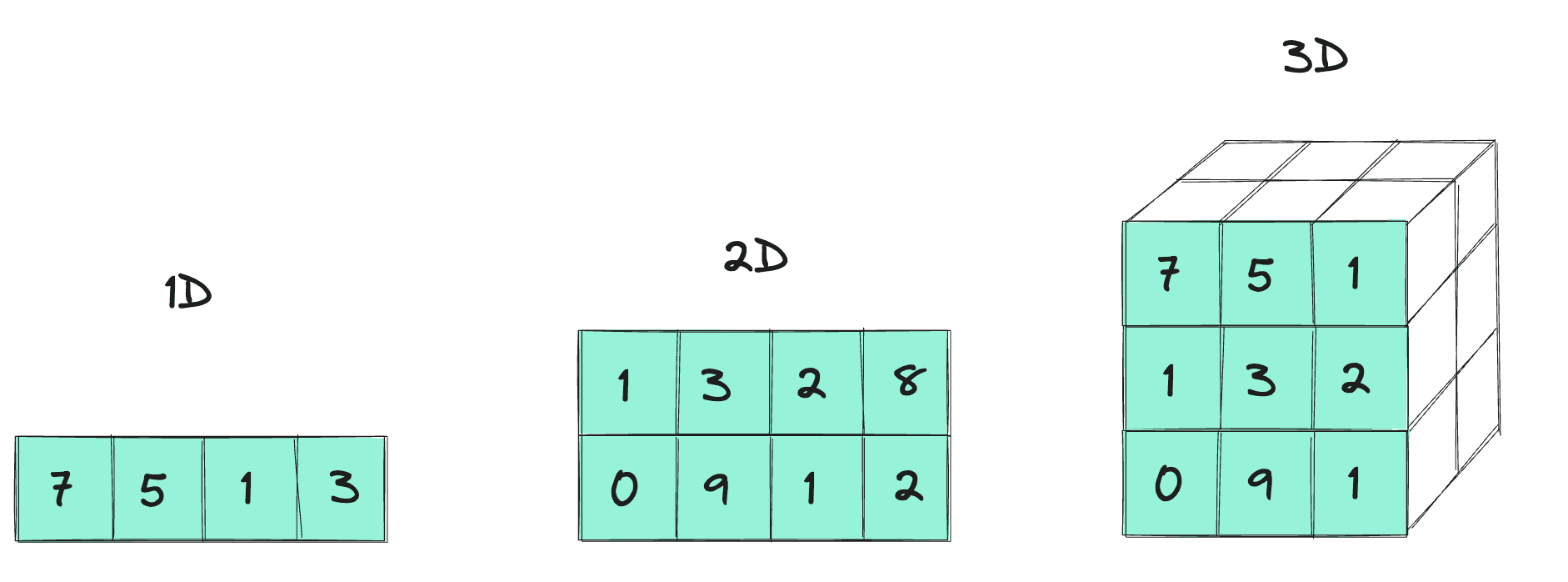
Arrays can come in different dimensions. The simplest form is a one-dimensional array, often called a vector (not really the vector used in math, but for now, we can think of it as a simple vector), which is like a single row of boxes. Each box holds one piece of data.
Additionally, arrays can be multi-dimensional, like matrices in mathematics. A two-dimensional array, for example, is like a grid of boxes, with rows and columns. Each box in the grid holds one piece of data, and you can access it using two indices: one for the row and one for the column.
Though arrays can have more than two dimensions, such as 3D arrays or higher, their use cases are relatively rare in typical programming scenarios. Therefore, in this blog, we won’t focus on them.
Static Array
Static arrays are like fixed-size boxes placed in a row or grid. Once you set the size, it doesn't change. They're handy when you know exactly how much space you need, like planning for a specific number of items in advance.
Static arrays are typically managed by the stack, meaning they're allocated and deallocated automatically as part of the program's execution flow. However, they can't grow or shrink, so you may end up with unused space if you allocate too much.
// Static array initialization in Java
int[] staticArray = {1, 2, 3, 4, 5};Dynamic Array
Dynamic arrays are more flexible. They're like magic boxes that can change size. If you need more space, they can expand; if you need less, they can shrink. This flexibility makes them great for situations where the number of items isn't known beforehand or may change over time.
Dynamic arrays are typically managed by the heap, which allows for more dynamic memory allocation. However, managing dynamic memory can be trickier and might lead to performance issues if not handled carefully.
Implementing a Dynamic Array from Scratch
Dynamic arrays are commonly utilized in high-level programming languages such as Python and JavaScript by default. In Java, there are also equivalents like List or ArrayList that provide dynamic array functionality. To better comprehend this concept, let's build our own dynamic array from scratch. I'll use Java (the language where I wrote my first "hello, world" program, heh), to implement it. Let's see:
public class DynamicArray {
private int capacity; // Capacity of the dynamic array
private int size; // Number of elements currently in the array
private int[] array; // Array to hold elements
// Constructor to initialize the dynamic array
public DynamicArray() {
capacity = 1; // Initial capacity
size = 0; // No elements initially
array = new int[capacity]; // Initialize the array with the initial capacity
}
// Method to add an element to the end of the array
public void push(int element) {
// Check if the array is full
if (size == capacity) {
// If full, double the capacity
resize(2 * capacity);
}
// Add the element to the end of the array
array[size] = element;
// Increment the size
size++;
}
// Method to remove and return the last element from the array
public int pop() {
// Check if the array is empty
if (size == 0) {
throw new IllegalStateException("Cannot pop from an empty array");
}
// Get the last element
int lastElement = array[size - 1];
// Decrement the size
size--;
// Return the last element
return lastElement;
}
// Method to resize the array to the new capacity
private void resize(int newCapacity) {
// Create a new array with the new capacity
int[] newArray = new int[newCapacity];
// Copy existing elements to the new array
for (int i = 0; i < size; i++) {
newArray[i] = array[i];
}
// Update the capacity and array reference
capacity = newCapacity;
array = newArray;
}
// Method to print the elements of the array
public void print() {
System.out.print("[");
for (int i = 0; i < size; i++) {
System.out.print(array[i]);
if (i < size - 1) {
System.out.print(", ");
}
}
System.out.println("]");
}
// Example usage
public static void main(String[] args) {
DynamicArray dynArray = new DynamicArray();
dynArray.push(1);
dynArray.push(2);
dynArray.push(3);
dynArray.print(); // Output: [1, 2, 3]
int poppedElement = dynArray.pop();
System.out.println("Popped Element: " + poppedElement); // Output: 3
dynArray.print(); // Output: [1, 2]
}
}Accessing
Accessing, also known as indexing, involves retrieving data from the array using indexes. Since all elements in an array occupy the same amount of space, accessing the address of any element within the array takes the same amount of time. Fetching a value via an index of the array is an arithmetic operation. All arithmetic operations are done in constant time, which is O(1). Not clear? Let's delve deeper:
We have the memory address of index 0 (also called the "Base address"). By adding the product of the index number (of the value to be accessed) and the size of element (e.g., the size of a short is 2 bytes) with the base address, we can obtain the address of that index’s value. We don’t have to iterate through the array. So it’s done in O(1).
Formula:
Address = base address + (index * size of element)Let’s take an example and apply:
short[] arr = new short[]{1, 2, 3, 4, 5};
System.out.println(arr[2]); // 3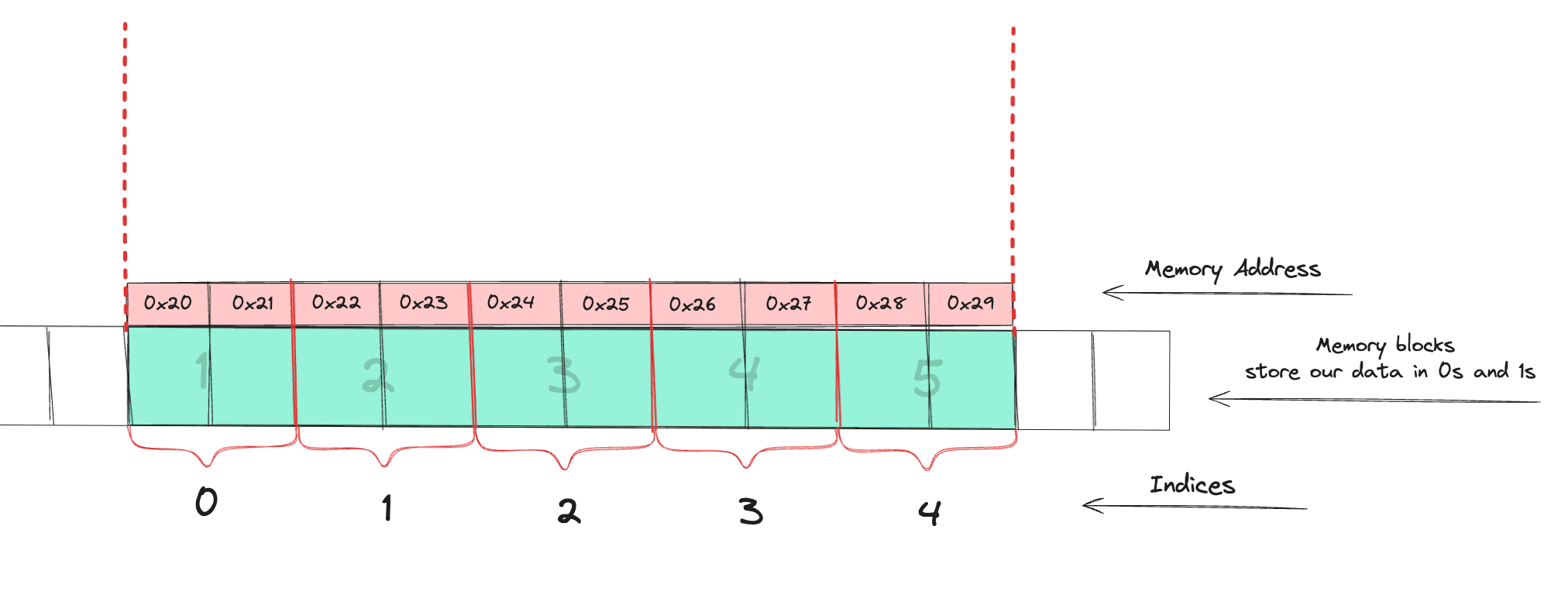
Now let’s break it down:
Address = base address + (index * size of element)
1. base address = 0x20
2. index = 2
3. size of element = 2 (short in bytes)
Address = 0x20 + (2 * 2)
Address = 0x24So what do we have in that memory address? Yaaay! The number 3. Easy, right? Yup, it is. I wish someone had explained this when we covered these topics in data structures and algorithms, rather than just saying it’s O(1) and that’s all.
Updating
Updating an element in a static array takes the same amount of time as accessing (O(1)). The same idea applies: we find the memory address and change the data in-place. For example:
arr[3] = 10; // this will change the value from 4 to 10
System.out.println(arr[3]); // 10Adding
Adding a new element to an array can be done either at the beginning or at the end of the array. However, in a static array with a fixed size, we cannot add new elements. We can perform these operations (adding at the end or beginning of the array) in a dynamic array, as its size can shrink and grow, as mentioned before with examples.
The whole idea behind adding elements to a dynamic array is about creating a new array with a different size, where all previous values plus the new value will move. This process is also known as insertion. If insertion occurs at the end of the array (achieved by methods like push in JavaScript, append in Python, or add in Java), it has a time complexity of O(1). This is actually an amortized time complexity (which is the average case rather than the worst case). Even though the array is copied and resized before adding the new element, it still has an amortized constant time complexity of O(1).
What about other cases? If we want to insert a new value at the beginning or in the middle of the array, the number of elements we need to shift depends on the position of insertion relative to the size of the array. On average, this takes O(n/2) time, which simplifies to O(n).
Above, we implemented a push function for a dynamic array. You can review the function and see how the addition operation is working.
Removing
Let's start with the static array again. As mentioned earlier, a static array has a fixed size, which means we cannot shrink or grow it. Instead, while removing an element, we can fill that position with zero or null, but the size remains the same. Which means it's not a good idea.
What about dynamic arrays? The case of dynamic arrays is similar to adding a new element. When removing from the end of the array (often accomplished with pop() in data structures like stack), it again takes O(1) time to perform, and of course, it's essential to mention that this is an amortized time complexity.
What about removing from the middle or the front of the array? The idea is similar to adding, but here, conversely, we move to the left side to fill the gaps created by the removed element. This operation takes linear time, O(n), where n is the number of elements in the array, because you have to shift every existing element one position to the left.
Here's a simple Java code demonstrating how removal can be achieved:
public static int[] remove(int[] arr, int index) {
// Base case: if array is empty or index is out of bounds, return original array
if (arr == null || index < 0 || index >= arr.length) {
return arr;
}
// Create a new array with size - 1
int[] newArr = new int[arr.length - 1];
// Copy elements from original array to the new array, skipping the element at the given index
for (int i = 0, j = 0; i < arr.length; i++) {
if (i != index) {
newArr[j++] = arr[i];
}
}
// Return the new array
return newArr;
}Conclusion
We've covered some fundamental operations commonly used with data in computing. The selection of a data structure for these operations depends on our knowledge of DSA. Here, we focused on arrays, the simplest data-structure. Arrays are incredibly useful, and having a deep understanding of them helps us grasp other data structures and algorithms well. In future blogs, we may explore more advanced data structures.
In my opinion, learning about data structures and algorithms isn't a waste of time. It helps improve your coding skills and provides you with more efficient ways to tackle programming tasks. So, don't hesitate to dive into learning about them next time! They're key to success in programming.
Happy coding!